リレー (Relays)
ブリッジでのリレーとは、何の情報も伝えないが経済的なビッドでパートナにその手のより詳しい情報を伝える機会を与えるためのビッドである。このアイデアは随分前からあり、皆に使われている1NTオープンに対するステイマン・コンベンションはその良い例である。
この章での説明はちょっと詳しすぎるときがあり、リレー・システムを使う予定のない読者にとっては決して重要なものではない。その意図するところは、リレー・ビッドを例示し、うまくいく時とそうでない時を示し、熱心にシステムをデザインしようとしている人のために面白いリレーのテクニックを提示することである。
リレー・ビッドの歴史
リレーをシステムに取り入れる度合いを変えることができるので、どこからそのシステムを「リレー・システム」と呼ぶかは意見の分かれるところである。最初の「リレー・システム」はおそらく、1950年代に世界選手権でピエール・ゲシュテムが使った「モナコ」であろう。
同じ頃、イタリアのシステム・デザイナーはこの問題と格闘していた。ディストリビューションに厳密なそのシステムでは、アンバランスな手はカナッペの原則に従ってビッドされた。最初にビッドしたスーツは2度目にビッドしたスーツより短く、2度目にビッドしたスーツは5枚以上を約束した。しかし、4441または5440の手は、どうビッドするのか。「ローマン・クラブ」では、これらのミニマムな手を2Cで、より強い手を2Dでオープンすることで解決した。「ナポリタン・クラブ」では、クラブ・スーツを示すために2Cオープンが必要になったので、ミニマムの3スータの手は1の台のスーツでオープンし、より強い手は2Dでオープンした。
ブリッジでの私の良い思い出のひとつは、ティーンエージャだった1970年の夏に教会の聖歌隊とロンドンを訪れたときのものだ。小さな書店で「ブルー・クラブ」の本を見つけたのである。それは、英語圏の人々が「ナポリタン・クラブ」の後継システムにはじめて出あったものであった。ベニート・ガロッツォとレオン・ヤルーズ共著の「Bridge de Competition」をReeseが翻案したものだった。それは啓示であった。そのシステムの洗練された素晴らしさ、完璧さに胸を打たれた。特に、「ブルーチーム2D」オープンとその後のリレー・システムにより、正確な形、強さ、コントロールの数とQの数を示すビッド・システムに感動したのである。未来を見た思いであった。
その後30年以上が経過し、リレーの技術は成熟してきた。多くのパートナシップが限定された状況でリレー・システムを使用している。一方、熱烈な愛好者は、「Ultimate Club」、「Super
Precision」、「MOSCITO」や「Viking Club」のような完全なリレー・システムを使用している。
言葉の定義
リレー・システムの議論に意味を持たせるために、使用する言葉の問題をまず明確にしておこう。一方は質問をし、他方が答える。それをどのように記述するか。多くの言葉が使われてきた。「キャプテン-操り人形」と「主人-召使」は誤解を生む。質問をする者をリレー者(Relayer)と呼び、Rで表すというのが人気がある。これがいい。レスポンダ(responder)がそのパートナを表すのに使われることがあるが、ブリッジでこの言葉はどちらかというと使われすぎているし、短縮形もうまく作れない。デービッド・モーガンに倣い、リレー・レスポンダ(Relay Responder)を使うことにし、RRと表す。リレー・ビッドかどうかの判断(relay determination) 規則によりどのビッドがリレーか判断する。また、より一般的に、どのビッドがどのリレーかを判断する規則がある、というのはリレーの種類は複数あるからである。単純なリレーのやり方では、各回で、決まった一連の質問を次々訊ねて行くリレーとなるビッドはただひとつだけである。単純なリレーのやり方でのリレー・ビッドかどうかの判断(relay determination) 規則は次のようになる。
リレーは、
・
最も安いビッドで、取り決めた最高のビッドまで(例えば6S)のビッド
・
最も安いビッド、取り決めた最高のビッドまでのビッド、ただし3NTは除く
・
最も安いビッド、ただしリレー者(relayer)が指定したスーツのゲーム・ビッドは除く
・
RRの一番短いスーツでの最も安いビッド
リレー・ビッドかどうかの判断(relay determination) 規則は、敵の介入を考慮にいれなければならない。ひとつのやり方は、介入がなかったら到達したであろうコントラクトより上に押し上げられなければリレーを続けるというものである。この前提でいくと、
・
RのLHOが3ステップ以上のビッドをしたときは、リレーは無し
・
RのLHOが1ステップまたは2ステップのビッドをしたときは、ダブルが1stステップ(リレー)、パスが2ndステップ、最も安いビッドが3rdステップ、・・・となる
・
RのLHOがダブルをかけたときは、リダブルが1stステップ(リレー)、パスが2ndステップ、最も安いビッドが3rdステップ、・・・となる
・
RのRHOがビッドしたときは、パスがリレーになる
連鎖破壊(breaking the chain)は、リレーでもサインオフでもないビッドをすることでリレー・プロセスを終了し、対話型ビッドを再開することを意味する。連鎖破壊ビッドは、ナチュラルにまたはアーティフィシャルに切札を決定するビッドになることがある。
ズーム(zoom)とは、ビッディング・スペースを節約するテクニックで、RRがリレーに対して最も高いビッドをすることになる状況で、次の質問を予測して両方に答えることをいう(考え方としてはさらにその先の質問にも答えることができるが、時に「支離滅裂ズーム(zoom out of control)」というリレーの落とし穴に落ちこむことがある)。この意味が不明でも今は気にしなくていい。実際どういうことかは最初の例で説明していく。
リレー開始ビッド(relay initiator)は最初のリレー・ビッドで、リレー・プロセスの始まりを告げるビッドである。「Ultimate Club」での例は、1の台のメジャ・スーツのオープンに対する2Cレスポンスはアーティフィシャルなゲーム・フォーシング・ビッドで、リレー開始ビッドである。
ディストリビューションを示す
例として、4333、4432または5332(マイナー5枚)の3つのディストリビューションに限定した1NTオープンを見てみよう。リレー開始ビッドはゲーム・フォーシングの2Cを使うことにし、「スペードカウント(spade-count)」と呼ぶ方式でディストリビューションを訊ねる。オープナは各スーツに何枚持っているかを、スペードから下方に順番に示していく。このために、まったくやむにやまれないある理由で、一時スーツの順番をハート、スペード、クラブ、ダイヤモンドの順(4Hから5Dまでのゲーム・コントラクトの順)にしていたことがある。今では、スペード・ファーストの方式が最も自然だと認識している(なぜなら、それがディストリビューションを表すときに使う方法だからである)。
1NT(15-17)
2C? (リレー開始ビッド)
2D S2、最低枚数
2H S3
声の抑揚を上げることではなく、伝統的に、?(クェッスチョン・マーク)がリレー・ビッドを示す。
Sの最高枚数は4枚なので、4枚のときはズームして次のスーツであるハート(H)の枚数を教える。
1NT
2C?
2S S4、H2
2NT S4、H3
S4でH4のときは、ズームしてダイヤモンド(D)の枚数を教える。こうして、完全なディストリビューションを教えることができる。
1NT
2C?
3C 4-4-2-3(Dの枚数にズームする)
3D以降 4-4-3-2
オープナのディストリビューションが完全にわかるまで、レスポンダのリレーは次のスーツの枚数質問を続ける。
1NT
2C?
2D S2
2H?
2S H3(最も安いビッド、M2-2はない)
2NT?
3C 2-3-3-5
3D 2-3-4-4
3H以降 2-3-5-3
この方式の最大の優位点は、違った状況にも適用可能であることである。あなたのシステムが1NTオープンに5枚メジャや6枚マイナを許したいとしても問題ない。このやり方で対応できる。
リレー・システム・デザイン
一つ前の章で、2NTから3NTまでの間で可能なビッド・シーケンスの数について考察した。ここではちょっと違ったことに興味が移る。2NTをビッドした人がRRならば、3NTを越えずにいくつのディストリビューションをRに教えることができるだろうか。3Cでリレーを始めるとして、RRは、3NTで1つのディストリビューションを、3Sで別のディストリビューションを教えることができる。RRのビッドが3Hなら、3NTを越えない答をすることができる質問のリレーはできないので、3Hもただひとつのディストリビューションを教えることにしか使えない。しかし、RRのビッドが3Dならば、3Hのリレーを使って、3Sまたは3NTのレスポンスにより、2つのディストリビューションを区別して教えることができる。
すなわち、2NTと3NTの間では、5つのディストリビューションを教えることができる。ステップ数毎に教えられるディストリビューションの数を連ねていくと、1、1、2、3、5、8、13、21、34、55、89、144、233、377、・・・。この有名な数列はうさぎの増殖を表しているとして、1202年に印刷された本にはじめて登場した。作者はピサのレオナルド・ピサロ(約1170-1250)で、フィボナッチ数列としての方が良く知られている。彼のことを聞いたことがないひとは、数学を勉強したことがないに違いない。「フィボナッチ季刊誌」さえ出ている。
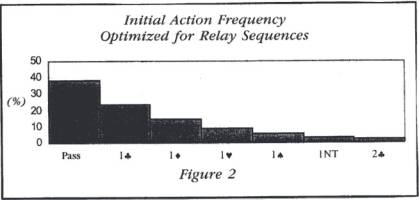
第三章(22ページ)で、ビッド可能なシーケンスを平等に割り振るようにデザインしたシステムの初期アクション確率の特徴を調べた。その結果、各オープニング・ビッドの使われる確率は、そのすぐ下のビッドの使われる確率の半分しかない。リレー・シーケンスだけに注目すれば、理想的な分布はフィボナッチ数列に基づいたよりフラットなものとなる。図2(Figure 2)でそれを示す。
もちろん、リレー・シーケンスだけを使うのは、ビッディング・スペースのひどく無駄使いになる。すべてのビッディング・スペースを使えば、リレー・システムははるかに効率的なものになる。2つの主なやり方がある。ひとつは、各回のリレーでひとつの質問ではなく複数の質問をすることである。Rは次に、最も知りたい質問をする。すなわち、最も安いリレー・ビッドで最もありそうで有益な質問をするようにシステムをデザインすること。ふたつめは、「連鎖破壊」をよくあることとして受け入れること。これを効率よくやるには、各回にRRが教える情報が、ありうる「連鎖破壊」をしなければならない場合にも有益なものであることを確実にすることである。例えば、1-4-2-6または7-3-3-0を示すビッドはどちらかわからなければ無価値なものである。しかし、常に5枚スペードと4枚ハートを示すビッドは、有益な情報であり、「連鎖破壊」をしなければならない場合にも有益なものである。ColoursFirst(まず長いスーツを示す)。
リレー・ビッディングの有効性
対話型が良いときもあれば、リレー・ビッディングが良いときもある。リレー・ビッディングは、先に取り上げた「ブルーチーム2D」、フラナリーまたはローマン2のような限定的な手を表すビッドに、強い手が相対しているときにはしばしば優位性がある。対話型は、ビッドの表すものが同一でないことから、ここでは明らかに不利である。手を教える上で、一方のパートナは他方よりはるかに簡単にできる。そこで、特別なオープニング・ビッドやレスポンスへの応答としてリレーが良く使われている。
ローマン、ナポリタン、ブルーチームの3スーター・ビッドは、システムの他のビッドで表せないディストリビューションを示すようにデザインされている。他のシステムの作成者は、3スータをどうビッドするかを単なる楽しみとして考えているように思われる。3スータに比べたら、例えばバランス・ハンドのオークションの方がはるかに重要なのは間違いないにもかかわらず、3スータ用にリレー方式がたくさんあるのはなぜかと思ったことはないですか。
リレー方式は、解決されなければならない場合の数が、そのために使えるビッド・スペースにうまく合致しているときに優位性を示す。あるビッドがバランス・ハンド、4333、4432または5332を示すならば、4333が4通り、4432と5332がそれぞれ12通り、全部で28通りのディストリビューションがある。それに比べて、4441は4通りしかない。議論のために、すべてのエース、キングとクイーンがどこにあるか特定しようとするとしよう。もし4333のディストリビューションだと、各スーツに8つの場合の数が存在する。すなわち、どれも無し、AKQ、Aのみ、Kのみ、Qのみ、AK、AQ、AKの8つである。全体では、8x8x8x8の場合の数がある(もちろん、点数の範囲からそのほとんどは除外されるが)。4441の場合には、シングルトンでは場合の数は4になり、全体では8x8x8x4になる。シングルトンにA、KまたはQはないと決めれば、全体の場合の数は8x8x8になる。
単純に言うと、シングルトンまたはボイドのある手は、区別される必要がある場合の数は減少する。リレーを使うシステムは、これを利用して、バランス・ハンドが質問をし、短いスーツのあるハンドが手を示すように作れる。この原則をShortnessShows(短いスーツある方が手を示す)と呼ぶ(Bridge Worldの1989年12月号、David
Morganの「The Balanced Hand Principle」参照)。
最善の方式は、リレー・テクニックが最適のところでそれを使い、対話型方式が最適のところでそれを使うものである。このことはあたりまえに聞えるかもしれないが、これを達成しているシステムはほとんどない。私は、ストロング・クラブ、1Dから2Hまでのオープニンヅ・ビッドは12-16HCPの限定ビッドという基盤の上にリレー・システムを載せたシステムをしばらくプレーした。限定ビッドへのレンポンダは、強い手のときは、リレーを使うか、対話型を使うか選択できた。リレーを使うのに最適の手は、絵札がたくさんある旧式の2NTオープンするバランス・ハンドによく似たハンドだと強く感じた。
なぜそう感じたのか考えてみよう。リレー・オークションはビッディング・スペースとの戦いである。最適のコントラクトを、そこを越える前に決定しなければならない、さもないとそのビッドがリレー・ビッドになってしまうためコントラクトとしてビッドできないという欲求不満に陥る。有用な概念は、安全レベル(safety level)という概念である。がっかりするレスポンスが返ってきても到達したいコントラクトのことである。2人の手を合わせれば6NTは保証されていることがわかっており、グランド・スラムを作るためにJの位置を探そうとしているならば、十分なビッディング・スペースがある。安全レベルがスーツでのゲーム・コントタクトならば、ビッディング・スペースはもっと少ないし、3NTならば、余裕をもって使うことができるビッディング・スペースはさらに制限される。4つから5つの好運な答が必要な時にリレー・シーケンスをしかけるのは、同様の当選確率で宝くじを買うようなものである。
RRからの情報は、完全に特定できる(「クラブとスペードのエースを持っている」)か、部分的にしか特定できないか(「2枚のエースを持っている」)のどちらかである。完全に特定できる情報は、Rの手とは無関係に即座に解釈できる。しかし、部分的にしか特定できない情報は、解釈できるかどうかはRの持ち手に依存する。「2枚のエース」は、自身が2枚のエースを持っているときにのみ特定できる。一般的に、Rが強ければ強いほど、バランスしていればいるほど、部分的にしか特定できない情報の解釈はしやすくなる。
バランス・ハンドがリレーした方がいいもうひとつの理由は、RRが短いスーツを示した時、3NTで止まるか、さらにビッドを続けるかの判断を、RRの短いスーツの自分の持ち方に依存して、Rは早期に決定できることにある。短いスーツを持っている側からそのような決定をするのはより難しい。もちろん、これは、リレーで何を訊ねるかによって一部変わってくるし、リレー方式はいまだ開発途中にある。「反スプリンタ(anti-splinter)」というものが最近開発され、短いスーツがあっても3NTに適した手であることを示すことができる。
リレー・オークションの明らかな有利性のひとつは、一方の手の内容がほとんど、あるいは完全にわからないためオープニング・リードが難しいことである。2004年イスタンブールでの第1ラウンド、対アイスランド戦で、イタリア選手のオープニング・リードには同情を禁じえない。
Board 6 KQ4
Dealer E 64
E-W vul. A764
A932
A752 J8
9
AKQ832
KJ953 Q8
764
KQJ
10963
J1075
102
1085
W N E S
Jorgensen Fantoni Armannson Nunes
1C1 P
2D2 P 2H3 P
2S4 P 2NT3 P
3H4 P 3NT all pass
1 ストロング
2 ナチュラル、ポジティブ
3 リレー
4 形を表す
ディクレアラーの手の情報がなく、サウスはH7をリード。簡単に9トリックを取られてしまった。逆のテーブルでは、通常のオークションのあとで、CリードのあとSシフトとなり、コントラクトは1ダウンした。
リレーする手がディクレアラーになると、優位性はオープニング・リードだけでなくプレーが終わるまで続く。アラン・ソンタグは、強い手がリレーをしてディクレアラーになることは約1/3トリック得する価値があると推定する。その価値は、多くのリレー愛好者が、リレーをする方ができるだけディクレアラーになるようにリレー方式をデザインさせるに十分である。
主流のリレー戦略
リレー方式をデザインする方法は数限りなくあるが、主流と考えられるのは次のものである。限定的な手であるメジャの1の台のオープンまたはストロング・クラブに対するナチュラル・ポジティブ・レスポンスなどの手が自分の手を教えるビッドをする、そしてパートナーがリレー開始ビッドをしてRになる。RRは、2ndスーツがあるかどうかといったディストリビューション情報をさらに教える。Rは、最も安いリレー・ビッドを続ける。RRは自分の正確なディストリビューションを教える。リレーがさらに続いたならば、RRは絵札の情報を教える。おそらく、総コントロール数(A=2、K=1)または総3-2-1ポイント(A=3、K=2、Q=1)からはじめて。次に、どこにあるか、その次はもっと下位の絵札へと進む。
パフォーマンスにおける人的要素
リレー方式を採用したペアは記憶とパフォーマンスの問題に対処する必要がある。コンピュータ・システムのデザインをしているならば、任意でどんなに複雑にしようとそれは自由であるが、人間が使うシステムの場合には、愛情のあるやさしい気遣いが必要である。単にシステムを覚えることができるというだけでは不十分である。リレーをする前に、可能なレスポンスのすべてを頭の中で思い浮かべ、どの答が返って来ても対処できるかどうか予測する必要がある。もし対処できない場合があるならば、連鎖破壊のビッドをした方がいいかもしれない。全体の過程を通じて、ディクレアラー・プレーをどうやっていくか考えながらビッドを続けていかなければならない。各ペアは、技術的完璧性を追求しながら、どれだけの複雑性を取り込むか自身で決めなければならない。より先進性のある方式を稚拙に使うより単純なシステムを巧みに使う方がはるかにいい。
アルゴリズムと専用システム
前に述べた「スペードカウント」方式は、規則に則っているという点でアルゴリズム型と呼べる。頭をそんなに使わずに様々の状況に適用できる。逆に、専用レスポンスは特定状況のために工夫される。フォーシング・ステイマンがその例である。
1NT
2D?
2H H4
2S S4、Hは4枚なし
2NT M4なし、m5もなし
3C C5
3D D5
伝統的にリレーシステムは、ナチュラルにすることでリレー構造をより快適で覚えやすいようにしてきた。レスポンスの種類が比較的少ないときにはこのやり方で満足できたが、一般的なリレーテクニックの基盤として使おうとすると頭の痛い問題が生じた。代替措置(ハートがリレースーツのときにハートスーツを示すためにNTで代替する)や、敵の介入に対処したり、ビッディング・スペースの節約のために要請事項をちょっと曲げ始めると、じきにつじつまをあわせるため例外状況のごたまぜになってしまう。そしてシステム・デザイナーにはナチュラルと思えるものでも、普通の人にはそう思われない。痛みをこらえ、アルゴリズムを定義し、ナチュラルであることを捨てたほうがいい。ジェフ・ルーベンスは、「Useful Space Principle」(Bridge
World、1980年11月号)という記事で次のように述べている:「ビッディング・スペースをどう利用するかをパートナ間で決めるときには、ナチュラル性やビッドの伝統的な意味にこだわらず、最も有益に使うようにすべきである。」
専用レスポンスの本当の価値は、レスポンスをパートナがパスしたいときにあらわれる。リレーシステムでは、リレーがゲーム・フォーシングを確立するのが普通であり、それは実に便利である。しかし、それはあらゆる状況で適格であるとはいえない。専用システムの例としては、4441を示すのに、シングルトンではなく、そのすぐ下のスーツをビッドするやり方がある。短いスーツのコントラクトになることは少ないのと、シングルトンのスーツのビッドを次のリレーとして使えると言う経済性を持っている。私の昔のリレーシステムにも別の例がある。1Dオープンは、12-16、バランスまたは3スータを示し、1Hレスポンスはインビテーション以上のリレー。これに対し、2の台のリビッドは3スータ、1NTはバランス、ミニマム、1Sはバランス、マキシマム。レスポンダは、1NTをパスしたければパスしていい。1Sに対するレスポンダの1NTは次のリレーになっていた。
リレー・レスポンスの最適化
リレーへのレスポンスを最適化するときに考えたいことのひとつは確率の高い順にレスポンスを割り振るということがある。例えば、1NTオープンの手で、スペードの枚数は、3枚の確率が一番高く、次が4枚、最後に2枚となっているので、その順番に答えるようにする。ここだけにしかこの考え方を採用しないならば、覚えにくくなるかもしれず、その価値は多分ないだろう。しかしシステム全体に適用するにはいい原則かもしれない。例えば、フラナリーを使うと仮定して、リレーに対し、ダイアモンドの枚数を示すレスポンスをするとする。しかし、ボイドはまれにしかないので、1ステップでボイドを示すのは無駄である。確率の順番(同率のときは、枚数の少ない方を優先)は、2、1、3、0、4である。確率理論に詳しいなら、このやり方を気に入るかもしれない。システム開発者の気まぐれな思いつきより不変の数学法則に則った方法には、正当性があるはずだ。ことが複雑になるのは、ズームを使っているときには、最も効率の悪いレスポンスは、可能性のあるビッドの最後のビッドではなく、そのひとつ前のビッドになる。人的要素を考慮し、理論的にも妥当な方式は、1枚を最初に、ボイドを最後に持ってきて、1、2、3、4、0の順番にすることだと私は思う。システムでは、ディストリビューションを完結できる場合が別の状況でも起こる。よくある状況は、RRがメイン・スーツが5枚以上で、少なくとも4枚のセカンド・スーツがメイン・スーツより長くないときである。2つのスーツの長さを確率の順に、5-4、5-5、6-4、6-5、などなどを確定させる。その後、訊かれたら、残りのスーツのうちより高い位のスーツの枚数を示す。メインとセカンド・スーツの長さの組み合わせのありえない組み合わせ(例えば、5-5のときはもう一方のスーツをビッドしたはずなどの理由で)は、レスポンスのリストからはずすことができる。長さの組み合わせが、ほんの一部しかはずせないならば、またそれゆえ確率がより低いならば、リストの順番を変更する価値はない。パートナのディストリビューションを正確に知ることは、Rにとって大きな価値がある。実際、徐々にリレー方式に移っていきたいと思っているなら、完全なディストリビューションがわかったあとでは、リレー・シークエンスに依存せず、いつでも対話型に切り替えることができる。良く使われるテクニックは、Rが、すくなくとも暫定的に切札を決めることである。これはステップ数でおこなわれる:1ステップは最も長いスーツを切札に決めるという意味で、2ステップは、次に長いスーツ、などなど、同じ長さのときは位の高低で決めていく。
絵札の特定
この時点で、RRは完全なディストリビューションを示した。全体のある程度の強さもわかっている必要がある。次のような質問を繰り返したくはない:「スペードのAを持っていますか、いいえ、ハートのAを持っていますか、いいえ、・・・何を持っているのですか、なぜなにももっていないの。」もし強さの範囲が広すぎるならば、ここでHCP、コントロールまたは3-2-1-ポイントをステップ・レスポンスで強さの範囲を狭めることができる。ここで開発されたやり方を使えば、その必要はなく、つぎの質問は「Aを示せ」というものになる。
Aを示すには、正確な位置ではなく、その枚数を不完全特定で示すのが普通である。ビッディング・スペースを節約するための妥協である。パートナ間ですべてのAを持っていることはよくあるが、もし2枚しかなければ、スラムねらいは終わり、安全な最終コントラクトを探さなければならない。もちろん、確実にAが1枚しか欠けていない場合には、どのAか知ることは大きな助けになる。サイド・スーツのコントロールのためにAが必要になる場合があり、またはその他の絵札との組み合わせでは、あるAより別のAの方がいい。例えば、D:xxx C:AxxとD:x C:KQxの組み合わせでは1ルーザーであるが、D:Axx C:xxxとD:x C:KQxの組み合わせでは2ルーザーになるかもしれない。しかし、Aを枚数で示すことは、良い妥協案であり、効率的で通常は効果的である。
ビッディング・スペースを節約するため、レスポンスに2つまたはそれ以上の意味を持たせることになることが多い。最初のブラックウッドでさえ5Cレスポンスは0または4枚のAを示す。4枚の違いは簡単に区別できるはずであり、Aが4枚とも無ければ、どっちにしろすでに高く上がりすぎている。3種類のA2枚を示す必要性からローマン・ブラックウッドが出てきたとき、さらに多くの意味を持たせる必要が生じた。今では、5Cが0/3、5Dが1/4を示し、そこではまだ安全な3枚の違いがあった。ローマン・キーカード・ブラックウッドでも、03/14(または14/03)を使用し、潜在的に強さの違いは2枚のAと切札のKをあわせたものの違いになる。レスポンスに意味を詰め込む例として、最後にイタリアン・ターボ4NTを見てみよう。そこでは、キーカードの数を偶数と奇数のグループに分けている。
レスポンスにより多くの意味を詰め込めば、誤解する確率も上がる。訓話として、0/4でさえ誤解された例をあげよう。
Q KJ43
KQJ83 10972
Q J9762
KQJ1093 -
W N E S
1C P 1D P
1H P 3H P
4NT P 5C P
7H X//
1971年の世界選手権でのできごとである。確かに、フランスはすでにファイナルへの資格を獲得していたし、3Hのビッドを真摯にうけとめられないペアがとんでもない間違いを犯したのであるが、それでも、「違いはわかるはず」と言われたとき、ちょっとは疑いの目で見てみるべきである。
不完全特定は、Aについてはかなりうまくいくが、K以下のカードについては同じことが言えない。ほとんどいつも、KまたはQなどを欠いており、切札がソリッドであること、またはトリックをとることができる可能性を知るために、どの絵札があるかを知る必要がある。絵札を特定する方法は複雑な問題であり、リレー・コミュニティでは活発な議論が交わされている。与えられた状況における最善の答は、次のような多くの要素に依存する。そもそも絵札についてどれだけ知っているか、リレーをする手とはどんな手か、リレー愛好者は、理想的なリレーシステムを目指してどれくらいの複雑さを受け入れるつもりか。真剣なリレー愛好者は、状況に合わせて最適化した動的な方法をよく使う。私は、もっと面倒くさくないアプローチを提示したい。理論的効率性と実践的実用性の間の良い妥協案である。
ディストリビューションが確定したあとの最初のレスポンスは、Aの枚数を偶数と奇数で区別したターボ・スタイルで示す。
1ステップ 0、2、または4枚のA
2ステップ(ズーム) 1または3枚のA
これはぎりぎりの選択であり、代わりに03/ 14/ 2方式を、常にまたはRRのビッドがあるしきい値を越えた時に使うことは完全に妥当な選択である。偶数/奇数の方式が安全とみなせる理由は、提示している方法では、Rは非常に強くてバランスした手を持っている場合が多いからである。絵札点が少ないが荒れた手でリレーをしてAの枚数を知りたいときには、正確な情報を得られない危険が増す。
Kやそれ以下の絵札は、否定キュービッド(denial cuebidding)の変形で示す。RRは頭の中で絵札の順列を次のように作る。まずKを長いスーツの順に、同じ長さのときは高い位の順に、二番目にQを、三番目にJを同様に順番に置いていく。シングルトンの絵札が格下げされる。シングルトンKはQのあとに来る。RRが最初に伝えるのは、その順列の最初の3つの絵札に関するものである。
1ステップ 0または3枚
2ステップ 1番目、または2番目と3番目
3ステップ 2番目、または1番目と3番目
4+ステップ(ズーム) 3番目、または1番目と2番目
4ステップの手を持っているときは、次のようにズームする。もし順列の4番目の絵札を持っているが5番目の絵札をもっていないときは、5ステップで止まる。答えようとしている絵札がなくなるまで、または順列の終わりにくるまで、ズームを続ける。最初のレスポンスのあと、Rは順列の次の3つの絵札について訊ねることができる。
Rが3つの絵札のうちどれか1枚持っていれば、答のあいまいさはなくなる。ひとつももっていないときには、いつでも連鎖破壊ができる。別のリレー方式も考えられるが、それを考える価値はないと思う。順列をどれだけ長くするか知っておく必要がある。さもないと、スペードのAが無いのに、9までの別の絵札があるために7NTまでいってしまうかもしれない。取り決めなしのときは、Jまででやめることにする。状況が変わると、この制限も変わってくるかもしれない。
例で見てみよう。あなたの手は、
S:KJ74 H:Q92 D:AKJ8 C:A7
パートナが1NT、15-17でオープンした。「スペード・カウント」リレー方式の2Cリレーをビッドする。パートナの答は3C。2D=S2、2H=S3、2S以上=S4のズームでHの枚数を示すので、2S=S4&H2、2NT=S4&H3、3C以上=S4&H4のズームでDの枚数を示す。ですから、3Cは、正確に4-4-2-3に違いない。つぎに絵札を訊くために3Dでリレーすると、3Hが返ってくる。3HはAの枚数が偶数枚、明らかに2枚である。そこで、パートナの絵札(KQJ)の順列を頭に思い描く。K、Q、Jの順に、それぞれ長いスーツの順で、同じ長さのときは高い位の順であるから、つぎのようになる。
SK HK CK/ DK SQ HQ/ CQ DQ SJ/ HJ CJ DJ
順列の最初の3枚の絵札について訊くため、3Sでリレーすると、パートナの答は4C。3NT=0または3枚すべて、4C=1番目、または2番目と3番目。SKは手にあるので、パートナはHKとCKを持っている。つぎの3枚について4Dでリレーすると、時間を賢く使っていたパートナは即座に4H=0または3枚すべてと答えた。あきらかに0枚である。さらに4Sでリレーすると、5D=2番目、または1番目と3番目が返ってくる。SJは手にあるので、DQを示す。最後の質問のため、5Hでリレーすると、パートナのビッドは5NT、HJに違いない。そこで、7Hをビッド。よくできました。
全部のビッドを下記する。
W E
A832 KJ74
AKJ8 Q92
Q3 AKJ8
K84 A7
1NT 2C?
3C1 3D?
3H2 3S?
4C3 4D?
4H4 4S?
5D5 5H?
5NT6 7H
1 4-4-2-3
2 偶数枚のA
3 SK、またはHKとCK
4 DK、SQ、HQのすべてまたは0枚
5 DQまたはCQとSJ
6 HJ、またはDJとCJ
もし、あなたがこれは簡単だと思ったら、あなたはよくできる。ほとんどの人は、練習しなければならないだろう。しかし、リレーにはまった人は、この種の実行力を身に付けることはできないことではないと証明している。